液体通过振动管道时的科里奥利相移效应
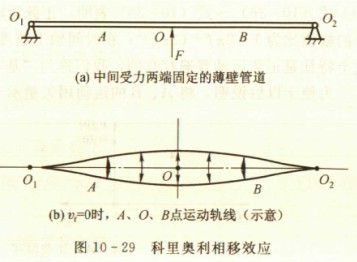
图10-29(a)中,O1、O2两点固定在一刚体上的薄璧弹性管道,在中心O点施外力使管道做微小的上下振动,频率f(角速度ω=2πf),管内有流体。设流体的流速vf=0,图10-29(b)表示此时管上各点的运动轨迹:除中心点O做垂直上下运动外,左侧各点做弧形运动,旋转中心在左侧;右侧各点做弧形运动,旋转中心在右侧。在A、B点处取轴长△x,这段流最质最为mf△x,管壁质量为M△x(M为单位长度管壁的质量)。在vf=0时,将这两点的运动表示成绕各自旋转中心的旋转,其角速度ωA(0)和ωB(0)(其中括号内0表示v1=0)的值相同:
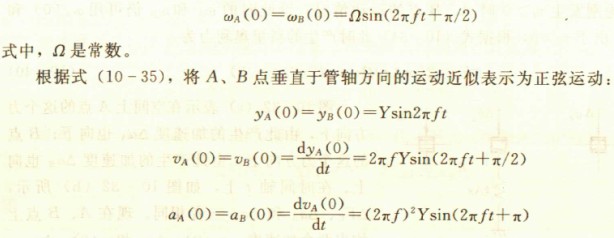
其中,y、v、a分别为垂直于O1O2轴的位移、速度和加速度,Y为常数。设A、B点的旋转半径为R(R≈r),由式(10-36)和式(10-38)得
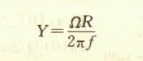
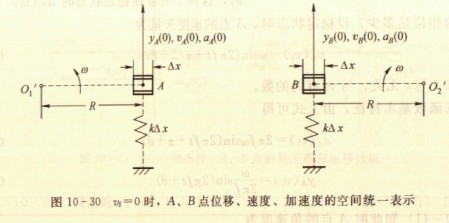
图10-30表示A、B点的上述运动。这个运动是由外力、管道和流体的质量以及管道弹性综合作用的结果。这图中用虚线表示的弹性力k△x,是为以后讨论vf>0时科里奥利力对A、B运动的影响,它表示管道O1O2的弹性在A、B点上此时对△x长管道运动产生的影响,k为常数。当A(或B)向上位移△y,弹性力向下,其值为k△x△y。
式(10-36)~式(10-38)表明,正弦运动具有这样的特征:位移、速度、加速度三者的幅值比为1:2πf:(2πf)2;在时间轴上速度比位移超前π/2,加速度比速度超前π/2。这个特征是正弦运动普遍存在的,我们称为“基本特征”.
为便于以后说明,将A、B的运动用矢量示于图10-31,其中t点为时间轴。






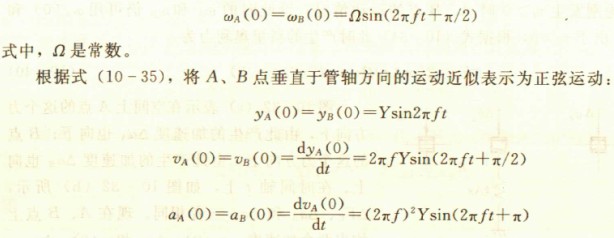
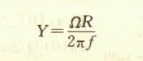 图10-30表示A、B点的上述运动。这个运动是由外力、管道和流体的质量以及管道弹性综合作用的结果。这图中用虚线表示的弹性力k△x,是为以后讨论vf>0时科里奥利力对A、B运动的影响,它表示管道O1O2的弹性在A、B点上此时对△x长管道运动产生的影响,k为常数。当A(或B)向上位移△y,弹性力向下,其值为k△x△y。
图10-30表示A、B点的上述运动。这个运动是由外力、管道和流体的质量以及管道弹性综合作用的结果。这图中用虚线表示的弹性力k△x,是为以后讨论vf>0时科里奥利力对A、B运动的影响,它表示管道O1O2的弹性在A、B点上此时对△x长管道运动产生的影响,k为常数。当A(或B)向上位移△y,弹性力向下,其值为k△x△y。



