科里奥利质量流量计的基本原理
当一个位于一旋转体内的质点作朝向或远离旋转中心的运动时,将产生一惯性力,原理如图5.1所示。当质量为兔的质点以匀速v围绕一个固定点P并以角速度。旋转的管道内移动时,这个质点将获得两个加速度分量:
①法向加速度a
r(向心加速度),其量值等于。ω
2r,方向朝向P点;
②切向加速度a
t(科里奥利加速度),其量值等于2ωv,方向与a
r垂直。

根据牛顿第二运动定律(力=质量X加速度),产生科里奥利加速度a
t,必定在a
t的方向上施加一个相应的力,其大小等于2ωvδ
m,这个力来自向上转动的管道。反向作用于管道上的力就是科里奥利力Fc=2ωvδ
m(简称科氏力)。从图5.1中可见,当密度为ρ的流体以恒定速度v向前流动时,任何一段长度为Ax的管道都将受到一个大小为△Fc的切向科氏力。
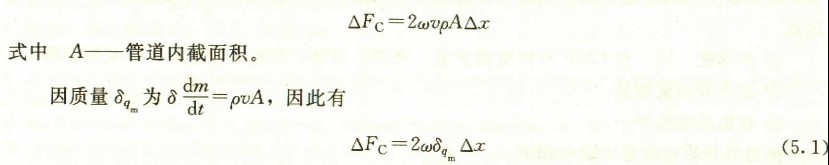
对于特定的旋转管道,其频率特性是一定的,△Fc仅取决于δ
qm。因此,直接或间接测得在旋转的管道中流动的流体所施加的科氏力就可以测得质量流量.这就是CMF的基本原理.
对商品化CMF设计,通过旋转运动产生惯性力是不切合实际的,而代之以使管道振动产生所需的力。当充满流体的管道以等于或接近其自然频率振动时,维持管道流动所需的驱动力是最小的。在多数CMF中,流体管道的两侧被固定,并在两个固定点的中间位置上振动,这就使管道的两个半段以相反的方向振动旋转。当无流量时,在检侧点相对位移的相位是相同的;当有流动时,科氏力所产生的附加的扭曲振动使得在检测点的相对运动有一个很小的相位差,这一相位差同质量流量成正比。
本文来自:
仪表商城 http://www.360abg.com


 根据牛顿第二运动定律(力=质量X加速度),产生科里奥利加速度at,必定在at的方向上施加一个相应的力,其大小等于2ωvδm,这个力来自向上转动的管道。反向作用于管道上的力就是科里奥利力Fc=2ωvδm(简称科氏力)。从图5.1中可见,当密度为ρ的流体以恒定速度v向前流动时,任何一段长度为Ax的管道都将受到一个大小为△Fc的切向科氏力。
根据牛顿第二运动定律(力=质量X加速度),产生科里奥利加速度at,必定在at的方向上施加一个相应的力,其大小等于2ωvδm,这个力来自向上转动的管道。反向作用于管道上的力就是科里奥利力Fc=2ωvδm(简称科氏力)。从图5.1中可见,当密度为ρ的流体以恒定速度v向前流动时,任何一段长度为Ax的管道都将受到一个大小为△Fc的切向科氏力。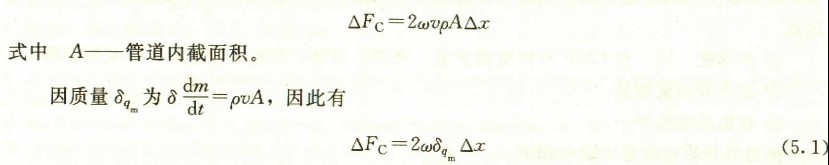 对于特定的旋转管道,其频率特性是一定的,△Fc仅取决于δqm。因此,直接或间接测得在旋转的管道中流动的流体所施加的科氏力就可以测得质量流量.这就是CMF的基本原理.
对于特定的旋转管道,其频率特性是一定的,△Fc仅取决于δqm。因此,直接或间接测得在旋转的管道中流动的流体所施加的科氏力就可以测得质量流量.这就是CMF的基本原理.


